2021. 2. 4. 20:44ㆍ배움엔 끝이없다/머신러닝
소프트웨어 전공을 한 사람이 머신러닝도 몰라서 되겠나? 라는 생각에 머신러닝 공부를 시작하게 됐습니다.
대학원생 정도까진 아니더라도 개념은 알아야 생각의 폭이 넓어지겠죠?
우선 친구한테 들을만한 강의를 추천받았습니다.
kaist.edwith.org/machinelearning1_17/lecture/40603
카이스트 문일철 교수님의 인공지능 및 기계학습 개론 강의입니다.
인공지능 쪽은 정말 하나도 모르지만, 이걸로 시작해보기로 했습니다.
우선은 이해한 대로 쭉 기록해 두고, 배우면서 잘못 알고 있던 점은 수정하는 방식으로 글을 써보겠습니다.
1. 이항분포(Binomial Distribution)
이번 강좌의 MLE와 MAP는 사건이 이항분포를 가진다는 전제하에 이루어집니다.
이항분포는 이산적인 사건(yes/no)을 n번 독립시행하는데 사건이 일어날 확률이 p일 때의 분포입니다.
동전을 10번 던져서 앞면이 0번~10번 나올 확률을 표현하면 이항분포로 됩니다.
사건의 횟수는 연속적이지 않기 때문에 불연속적인(discrete) 그래프가 나옵니다.
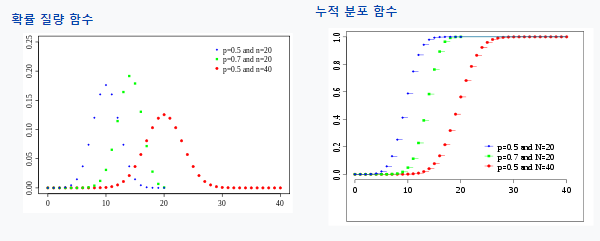
이항 분포의 매개변수(Parameter)는 시행 횟수 n과 사건이 일어날 확률 p가 있고, 이 두 가지에 따라 그래프가 바뀝니다.
그럼 "x축: 몇 번 일어날 건가?" 에서 몇 번이 확률변수 K인 것 같습니다.
그러니까 n, p는 함수를 결정짓는 parameter고, k는 그 함수에서 어떤 값을 가져올 거냐에 대한 parameter입니다.
이항 분포를 식으로 나타내면 이렇습니다.
$$Pr(K=k)=f(k;n,p)=\binom{n}{k}p^k(1-p)^{n-k},$$
$$\binom{n}{k}=nCk=\frac{n!}{k!(n-k)!}$$
확률이 p인 사건이 k번 일어나고 n-k번 안 일어나야 하고( \(p^k(1-p)^{n-k}\) ), 순서에 따른 경우의 수를 곱해주면 됩니다. ( \(nCr\) )
2. MLE(Maximum Likelihood Estimation)와 MAP(Maximum a Posteriori Estimation) 예시 상황
MLE와 MAP는 이항 분포를 가지는 사건이 일어난 확률인 p를 구하는 방법론들입니다.
MLE는 어떤 데이터가 나왔을 확률이 가장 높은 확률 분포를 찾는 방법,
MAP는 MLE와 같은 방법으로 찾지만 확률에 대한 사전지식을 첨가할 수 있는 방법입니다.
-동전 예시
앞면이 나올 확률이 p인 동전을 n번 던져서 앞면이 k번 나올 확률은 이항 분포의 형태를 가집니다.
동전을 5번 던져서 H(앞면)와 T(뒷면)이 HHTHT의 순서로 나왔다고 하고,
관측된 데이터를 근거로 동전이 앞면이 나올 확률을 구해보겠습니다.
-변수 정의
\(D\) : 관측된 데이터로, 이 예시에선 HTHHT이지만 앞면 3번과 뒷면 2번으로 간주합니다. (순서 상관 X)
\(\alpha_H, \alpha_T\) : 사건이 일어난 횟수와 일어나지 않은 횟수로, 이 예시에선 앞면(H)이 나온 횟수와 뒷면(T)이 나온 횟수
\(\theta\) : 사건이 일어날 확률로, 이 예시에선 동전을 던졌을 때 앞면이 나올 확률
\(P(D|\theta)\) : 사건이 일어날 확률 \(\theta\)가 주어졌을 때 데이터 \(D\)가 관측될 확률
지금 데이터 \(D\)가 순서 상관없이 앞면이 3번 나온 경우이기 때문에 위의 이항분포 식에서 \(nCk\) 부분을 빼주고
변수 이름을 알맞게 바꿔주면 아래와 같이 표현할 수 있습니다.
$$P(D|\theta) = \theta^{\alpha_H}(1-\theta)^{\alpha_T}$$
여기서 목표는 정답이 되는 \(\theta\)를 찾는 겁니다.
3. MLE로 찾기
MLE는 어떤 데이터가 나왔을 확률이 가장 높은 확률 분포를 찾는 방법입니다.
-방법 요약
\(P(D|\theta)\)를 최대로 만드는 \(\theta\)를 찾는다.
\(P(D|\theta)\)에 자연로그를 취하고 미분을 이용해 극대점에서의 \(\theta\)를 찾으면 된다.
-실행 내용
\(P(D|\theta)\)를 최대로 만드는 \(\theta\)를 \(\hat{\theta}\)라하고, 이렇게 표현합니다.
$$\hat{\theta}=argmax_{\theta}P(D|\theta)$$
여기서 \(\hat{\theta}\)를 구하기 위해 미분과 로그를 이용한 기가 막힌 방법을 사용합니다.
최댓값일 때 \(\theta\)의 값을 구하기 위해 미분을 해 도함수의 값이 0일 때 \(\theta\)값을 구합니다.
\(P(D|\theta)\)의 확률분포가 이항분포를 따른다고 했기 때문에 도함수가 0인 지점이 극대점일 것입니다.
또, 자연로그 함수는 증가함수기 때문에, 미분을 편하게 하기 위해 \(P(D|\theta)\)와 자연로그를 합성해
$$argmax_{\theta}P(D|\theta) = argmax_{\theta}lnP(D|\theta)$$
를 만들 수 있고, 이 함수를 미분해서 0이 되는 지점을 찾으면
$$\frac{d}{d\theta}(lnP(D|\theta)) = 0$$
$$\frac{d}{d\theta}(ln(\theta^{\alpha_H}(1-\theta)^{\alpha_T})) = 0$$
$$\frac{d}{d\theta}(\alpha_Hln\theta+\alpha_Tln(1-\theta)) = 0$$
$$\theta = \frac{\alpha_H}{\alpha_T+\alpha_H}$$
즉, 동전이 앞면이 나올 확률은 (앞면이 나온 횟수) / (총 던진 횟수)가 됩니다.
이거를 나중엔 다른 분포에도 적용할 수 있을 것 같습니다.
4. MAP로 찾기
MAP는 MLE와 같은 방식이지만, \(\theta\)에 관한 사전정보를 첨가할 수 있습니다.
-방법 요약
\(P(D|\theta\)에 사전정보 \(P(\theta)\)를 첨가해 \(P(\theta|D)\)를 만든다.
\(P(\theta|D)\)를 최대로 만드는 \(\theta\)를 찾는다.
\(P(\theta|D)\)를 비례식으로 표현하고 자연로그를 취하고 미분을 이용해 극대점에서의 \(\theta\)를 찾으면 된다.
-실행 내용
*이 부분은 강의에서 자세히 다루지 않아서 그냥 받아들였습니다*
위 MLE로 동전이 앞면이 나올 확률이 60%라고 구했지만, 사실 저희는 50%라고 알고 있습니다.
이와 같은 사전 정보는 아래 공식에 의해 첨가됩니다.
$$P(\theta|D)=\frac{P(D|\theta)P(\theta)}{P(D)}$$
위 공식을 이렇게 해석합니다.
$$Posterior = \frac{Likelihood * Prior Knowledge}{Normalizing Constant}$$
여기서 \(P(\theta|D)\)는 데이터가 관측됐을 때 \(\theta\)의 확률(?)이고,
\(P(\theta)\)는 사전 정보, \(P(D)\)는 \(D\)가 관측될 확률입니다.
여기서 \(P(D)\)는 상수로 취급되기 때문에 비례식으로 표현됩니다.
$$P(\theta|D)∝P(D|\theta)P(\theta)$$
여기서도 MLE와 비슷하게 \(\hat{\theta}=argmax_{\theta}P(\theta|D)\)를 찾아야 합니다.
사전정보 \(P(\theta)\)는 베타 분포로 표현하게 되는데, 아래가 베타분포 식입니다.
$$P(\theta) = \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha,\beta)}, B(\alpha,\beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}, \Gamma(\alpha) = (\alpha-1)!$$
어차피 미분해서 극대점만 찾으면 되기 때문에 \(\theta\)와 관련된 식들만 뽑아서 정리하면,
$$P(\theta|D)∝\theta^{\alpha_H+\alpha+1}(1-\theta)^{\alpha_T+\beta-1}$$
이렇게 됩니다.
아까 MLE의 방식과 같이 자연로그를 취하고 극대점을 구하면,
$$\hat{\theta} = \frac{\alpha_H+\alpha-1}{\alpha_T+\alpha_H+\alpha+\beta+2} $$
이렇게 \(\hat{\theta}\)를 구할 수 있습니다.
이를 해석하면 \(\alpha\)와 \(\beta\)는 사전 정보와 관련된 변수이므로, MLE의 결과에 사전정보가 첨가된 것을 알 수 있습니다.
이 \(\alpha\)와 \(\beta\)를 결정하는 방법은 .. 베타 분포에 대해 알아야 할 것 같은데, 지금은 중요하지 않은 것 같아 넘어갔습니다.
5. MLE와 MAP의 비교
$$\theta = \frac{\alpha_H}{\alpha_T+\alpha_H}$$
$$\hat{\theta} = \frac{\alpha_H+\alpha-1}{\alpha_T+\alpha_H+\alpha+\beta+2} $$
MLE의 경우 오로지 주어진 데이터만 활용해 \(\theta\)를 구했고, MAP는 거기에 사전정보가 추가됐습니다.
하지만 시행 횟수(\(\alpha_H+\alpha_T\))가 커지면 커질수록, MAP에서의 \(\alpha\)와 \(\beta\)의 영향력은 줄어듭니다.
그래서 시행 횟수가 늘어날수록 사전정보의 영향력이 줄어들어 MLE와 MAP로 구한 \(\hat{\theta}\)의 값이 같아집니다.
6. Error Bound, PAC Learning
오차 범위를 나타내는 공식이 있어 적어두겠습니다.
$$P(|\hat{\theta}-\theta^*| \le \varepsilon) \ge 2e^{-2N\varepsilon^2}$$
여기서 \(\varepsilon\)은 오차, \(\theta^*\)는 정답 \(theta\)의 값, \(N\)은 시행 횟수입니다.
\(N\)이 커지면 커질수록, 오차가 줄어듭니다.
이를 활용하면 예를 들어 오차가 0.1 이상일 확률이 0.01% 미만으로 만들어주는 시행 횟수를 정할 수가 있습니다.
위 식을 이용해 "이 정도면 맞다"라고 하면서 학습 하는 게 PAC(Probably Approximately Correct) Learning이라고 합니다.
'배움엔 끝이없다 > 머신러닝' 카테고리의 다른 글
| [논문 읽기] Where and Who? Automatic Semantic-Aware Person Composition (0) | 2023.08.28 |
|---|---|
| [논문 읽기] MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications (0) | 2023.07.20 |
| [논문 읽기] Camera View Adjustment Prediction for Improving Image Composition (0) | 2023.07.01 |
| 인공지능 관련 용어정리 (0) | 2021.10.22 |
| 머신러닝 배워보자 (2) Decision Tree (Rule Based Learning) (0) | 2021.02.08 |